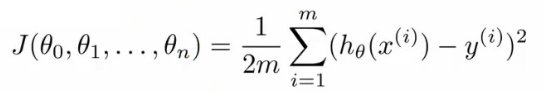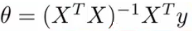When putting you’re home for sale on the real estate market, researching sale prices is always necessary. You can rely on realtors experience in a geographic area, use Zillow’s Zestimate or troll through listings on various real estate web sites to make somewhat educated guesses. Your best bet is probably to hire a professional. For me, it was of interest to build a model for predicting a price based on other homes for sale in the area.
The goal was to:
- collect geographically local property data on other properties for sale
- build a mathematical model with sample data representative of the property attributes
- plug in the corresponding attributes of my house to predict a sale price
The number of houses on the market change on a daily basis as can the prices during the sale period. I wanted the ability to quickly pull current data, build a model and predict a price at anytime so I implemented the following:
- a script to scrape data from realtor.com
- code to build a model with property attributes using multi-variant linear regression
- the ability to input the corresponding property attributes of my house into the model to predict a sale price
Scraping Data
The data is scraped from realtor.com. This web site allows looking at properties for sale in localized geographic region. Data could be scraped for many geographic regions creating a large data sample or you can scope the data to an area where fewer property attributes become more relevant. Many people reference Zestimate for home price estimates. For my neighborhood, for example, the estimates are too low. Other neighborhoods have estimates much too high. I suspect the algorithm used is very general and doesn’t account for geographic uniqueness. Relevant attributes unique to my geographic area are gorgeous mountain views. Some properties have exceptional mountain views, others do not. I choose to scope the the area of data used for the training set to roughly a 5 mile radius. The actual boundaries are set by realtor.com. The number of properties for sale in the area currently averages about 140. A small set for high accuracy but turned out to be big enough to get an estimate comparable to professional advice.
Scraping data for the training set is done using Python and the BeautifulSoup package to help parse the page content. The flow of execution implemented is roughly:
Open a file for output
load the realtor.com local region page
while there are more properties to read:
read property data block
parse the desired attribute values
write attributes to output file
if at end of listing page:
if there are more pages:
load next page
close output file
Executing the script produces a file with content looking like:
5845 Wisteria Dr city st zip Homestar Properties, 234900, 4, 3, 1225, 88 165 Timber Dr city st zip, The Platinum Group, 1200000, 7, 5, 7694, 520 6380 Winter Haven Dr city st zip Pink Realty Inc., 544686, 4, 4, 5422, 25 ...
The columns correspond to address, realtor name, price, # of bedrooms, # of bathrooms, square footage and acreage. Additional values not shown here are year built, whether or not the property has a view, kitchen is update or not, bathroom is updated or not. The acreage value is multiplied by 100 in the output file to produce an integer value for easier matrix arithmetic. The address and realtor name is not used in the building of the model, however it is useful when comparing page scrapes to determine which properties are new to the list and which ones have sold.
Building the Model
The output file from the web page scrape becomes the training set used to build the model. I used multi-variant linear regression to build the model. It is a reasonable approach for supervised learning where there are many attribute inputs and one calculated value output. In this case the predicted price is the output.
The hypothesis defining the function used to predict the price is
hθ(x) = θ0 + θ1x1 + θ2x2 + θ3x3 + θ4x4
where
- h is the hypothesis
- the right side of the equation is the algorithm to determine the hypothesis
- x’s represent the attributes of the property and
- θ’s are the parameters used to define the gradient in a gradient descent algorithm
The gradient descent algorithm minimizes over all θ‘s meaning an iteration over all θ parameters is done to find, on average, the minimal deviation of all x’s from y (the price) in the hypothesis function. The equation for calculating the minimum cost (or deviation) looks like:
where J is the cost function. Fortunately this equation can be solved computationally with linear algebra in a straight forward manner. Creating a feature vector of all attributes for each training example and building a design matrix X from the vectors, θ value can be solve for using
Currently I’m learning some about the Octave language. With much learning and experimentation (on my part), the code is relatively straight forward. The code first reads in the trainingg set data file and normalizes each feature dimension. Normalization is done by subtracting the mean of the feature values and subtracting that from each element and then dividing each element by 1 standard deviation of the feature values. The important parts of the rest of the gradient descent code looks like:
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
theta = theta .- alpha * (1/m) * (((X*theta) - y)' * X)';
J_history(iter) = (1/(2*m)) * (X*theta-y)' * (X*theta-y);
end
where X is the matrix of normalized feature vectors and J_history is the cost function value. The cost function value is plotted to validate the function is converging to a minimized solution. The plot looks like the following over 400 iterations
Also for a simple visualization, a two dimensional plot of square footage vs price gives an idea of how the model performs using one feature. Basically a simple limear regresion fit using gradient descent.
Retrospective
The cost function appears to converge nicely on the training set and a simple visual plot indicates a reasonable fit. To predict prices for a given feature set, the Octave code looks like:
v=[4793, 5, 4, 66, 1986];
price = [1, (v-mu)./sigma] * theta;
where
- v is the vector of feature values representing the property and
- price is calculated as the vector normalized using the same values to normalize the training data multiplied by the vector of theta values representing the hypothesis function.
Getting predictive price results for a set of property attributes has produced values comparable to professional opinion. So the model turns out to be fairly accurate. Many more attributes could be added to the model theoretically making the model more accurate. Although it can become time consuming to acquire all the attributes if they are not readily available. I believe scoping training data sets to bounded geographic areas increases accuracy, especially if you can pick unique attributes relevant to the area. Who knows, maybe a tool like this could be used to make accurate price predictions available for use by most everyone.